SVD dan Digit Recognition

Saat sedang menulis post terakhir mengenai Dekomposisi Nilai Singular, saya ingat bahwa dulu saat S1 saya pernah mengerjakan suatu projek kuliah yang berhubungan dengan SVD. Akhirnya, didorong oleh keinginan luhur, saya cari dan ketemulah di Google Drive. Waktu semester 7 di Bogor, saya mengambil mata kuliah Matematika Komputasi dimana ada tugas akhir yang harus dikerjakan berkelompok. Karena saya adalah ketua kelompok yang semena-mena, tentu saja dengan sebelah pihak saya memutuskan topik mengenai dekomposisi matriks dan aplikasinya bersama dengan 3 orang teman sekelompok.

Kita sepakat (saya sepakat dan teman-teman saya terpaksa) untuk mengambil satu bab dari buku yang direkomendasikan oleh dosen kami. Bab tersebut membahas mengenai SVD dan aplikasinya untuk pengenalan digit. Setelah saya lihat kembali, ternyata saya menggunakan R dan bukan Python dalam projek tersebut. Karena saya malas untuk porting, maka di tulisan ini saya akan menulis code tetap dalam bahasa R.

Table of Contents

Pengenalan Data

Data yang kami gunakan adalah data berupa tulisan angka dalam bentuk matriks yang dapat diunduh di sini. Disana ada 4 buah file yang dapat di-download yaitu file train-images dan train-labels yang berisi 60.000 gambar berupa matriks dan juga label (digit 0-9) dari setiap gambar di data sebelumnya, dua file lainnya adalah test-images dan test-labels yang berisi 10.000 gambar matriks dan juga labelnya. Setiap gambar merupakan matriks berukuran $28 \times 28$ yang merepresentasikan suatu digit. Contoh matriks yang merepresentasikan digit 1 sampai 3 ditunjukkan di bawah ini.

Tujuan dari projek ini adalah menggunakan Dekomposisi Nilai Singular untuk mendapatkan komponen utama dari setiap digit pada training data lalu menggunakan komponen-komponen utama setiap digit untuk memprediksi digit-digit pada test data dan lalu membandingkannya. Target kami awalnya adalah mendapatkan akurasi 80% atau lebih dengan menggunakan cara ini.

Digit Recognition

Secara garis besar yang kami lakukan adalah sebagai berikut:

• Data training kami bagi menjadi 10 kategori berdasarkan labelnya (digit 0-9).
• Untuk setiap kategori digit, kami buat sebuah matriks besar yang setiap kolomnya merepresentasikan satu buah digit tulisan tangan.
• Melakukan SVD pada setiap kategori digit (jadi ada 10 SVD yang dihasilkan).
• Ambil komponen utama setiap dari setiap SVD dengan jumlah yang sudah ditentukan sebelumnya.
• Untuk setiap gambar di test data, cari jaraknya ke komponen utama setiap kategori (jadi kita dapat 10 nilai jarak).
• Kita prediksi gambar itu sebagai digit dengan jarak terkecil dibandingkan kategori lainnya.

Step yang pertama dapat dilakukan dengan mudah. Step yang kedua dapat dijelaskan sebagai berikut: misal gambar yang kita miliki hanya berukuran $3 \times 3$ maka akan kita buat vektor dengan panjang 9 seperti yang ditunjukkan di bawah ini.

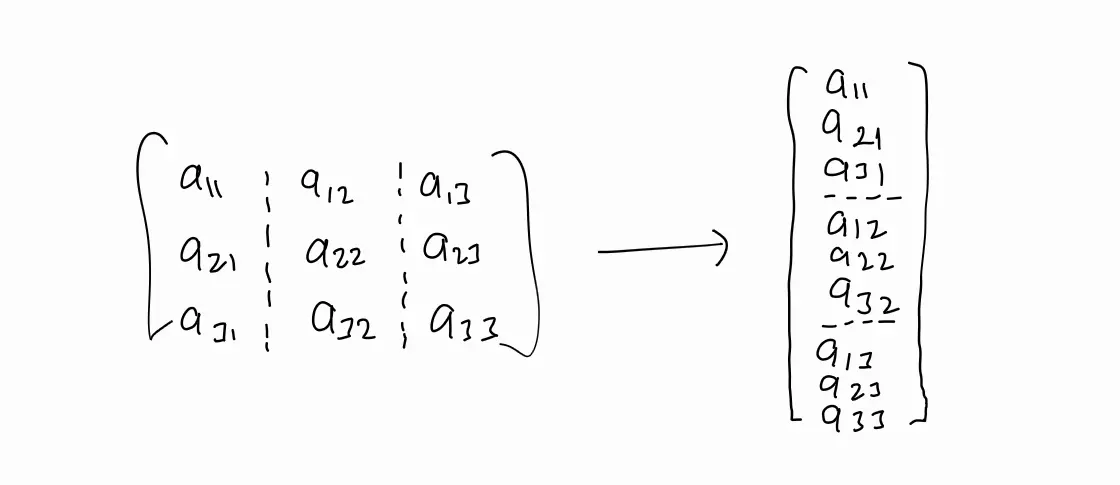
Sehingga jika, misal kita memiliki 1000 gambar dari suatu digit dan setiap gambar digit berukuran $28 \times 28$, maka kita akan memiliki suatu matriks berukuran $784 \times 1000$ (karena $28 \times 28 = 784$).

Selanjutnya kita akan melakukan SVD pada setiap matriks yang kita peroleh sebelumnya. Ingat kembali bahwa SVD merupakan dekomposisi matriks $A$ menjadi $A = UDV^*$ dimana $U \in \mathbb{C}^{m \times r}$ dan $V \in \mathbb{n \times r}$ merupakan matriks dengan kolom ortonormal dan $D$ matriks diagonal dengan unsur-unsur diagonal bilangan positif dengan $r=\text{rank}(A)$. Berkaitan dengan ruang kolom dan ruang baris dari $A$, kita punya teorema berikut.

Misal $A \in \mathbb{C}^{m \times n}$ memiliki dekomposisi nilai singular $A=UDV^*$ seperti yang disebutkan di atas. Maka

• Kolom-kolom dari matriks $U$ membentuk basis bagi ruang kolom matriks $A$.
• Kolom-kolom dari matriks $V$ membentuk basis bagi ruang baris matriks $A$.

Perhatikan bahwa kita menyusun sebuah matriks dimana kolom-kolomnya menyatakan gambar dari suatu digit. Sehingga kita bisa mengasumsikan bahwa ruang kolom dari matriks ini menyatakan ruang dari semua gambar digit tertentu dari data training. Akibatnya kolom-kolom dari matriks $U$ merupakan basis bagi ruang digit ini. Dengan mengambil beberapa vektor kolom dari $U$ yang bersesuaian dengan nilai singular yang besar, kita harapkan untuk mendapatkan vektor basis yang berpengaruh besar terhadap ruang digit tersebut. Pada kasus ini kita mengambil $n=10$ vektor pertama dari $U$.

n <- 10
for (i in 0:9) {
  digit_matrix <- train_images[,train_labels==i]
  SVD <- svd(digit_matrix); SVD_list[[i+1]] <- SVD
  U_truncated <- SVD$u[,1:n]
  distance_matrix_list[[i+1]] <- diag(dim(train_images)[1])-U_truncated %*% t(U_truncated)
}

Selanjutnya kita akan menjelaskan baris terakhir pada kode di atas. Kita sudah dapatkan suatu subruang yang kita harap dapat menjelaskan ruang dari suatu digit. Untuk suatu vektor gambar sebarang, kita akan menghitung jarak dari vektor tersebut ke masing-masing subruang (terdapat 10 subruang). Bagaimana cara mencari jarak dari suatu vektor ke subruang tertentu? Kita akan gunakan teorema-teorema berikut.

Misal $S$ suatu subruang tak-nol dari $\mathbb{C}^{n}$ dan misal $x \in S$. Maka $x$ dapat ditulis sebagai $x = x_S + x_{S^\perp}$ dimana $x_S \in S$ dan $x_{S^\perp} \in S^\perp$. Penulisan tersebut disebut dengan dekomposisi ortogonal dari $x$ dan vektor $x_S$ disebut dengan projeksi ortogonal dari $x$ pada $S$.

dan

Misal $S$ suatu subruang tak-nol dari $\mathbb{C}^{n}$ dan misal $x \in S$.

• Projeksi ortogonal $x$ pada $S$, misal $x_S$, adalah vektor di $S$ yang memiliki jarak terdekat $x$.
• Jarak dari $x$ ke subruang $S$ adalah $||x-x_S|| = ||x_{S^\perp}||$.

Perhatikan bahwa matriks $U$ yang kita peroleh dari hasil SVD merupakan suatu matriks dengan kolom-kolom ortonormal. Mencari projeksi ortogonal dari suatu vektor pada subruang berupa ruang kolom suatu matriks diberikan di bawah ini.

Misal $A \in \mathbb{C}^{m \times n}$ merupakan matriks dengan kolom-kolom yang bebas linear dan misal $S$ ruang kolom dari matriks $A$. Maka $A^*A$ invertibel dan projeksi ortogonal dari $x \in \mathbb{C}^m$ pada $S$ adalah $x_S = A(A^*A)^{-1}A^*x$.

(Rasanya pernah liat ekspresi $A(A^TA)^{-1}A$ dimana ya???) Karena matriks $U$ yang kita miliki merupakan matriks dengan kolom-kolom ortonormal, maka projeksi ortogonal dari $x$ pada ruang kolom $U$ adalah $x_S=UU^*x$. Sehingga jarak dari suatu vektor $x$ ke ruang kolom dari $U$ adalah $||x-x_S|| = ||x-UU^*x|| = ||(I-UU^*)x||$. Hal ini menjelaskan pengambilan matriks $(I-UU^*)$ pada kode di atas.

Sehingga sekarang untuk setiap vektor di test data, kita akan hitung nilai dari $||(I-U_iU_i^*)x||$ untuk $i=0,1,2,\ldots,9$. Setelahnya, kita ambil label hasil prediksi sebagai label dengan norma terkecil.

for (j in 1:dim(test_images)[2]) {
  digit_vector <- test_images[,j]
  min_distance <- 0
  temp_label <- 0
  # compute distance for each digit category
  for (i in 0:9) {
    distance <- norm(distance_matrix_list[[i+1]] %*% digit_vector)
    if (i==0) {
      min_distance <- distance
    }
    else if (distance < min_distance) {
      min_distance <- distance; temp_label <- i
    }
  }
  label_result[j] <- temp_label
}

Bagian terakhir adalah bagian yang paling penting, yaitu menghitung akurasi. Apakah algoritma coba-coba yang kita buat ini cukup baik?

accuracy <- mean(label_result==test_labels)
print(paste("The accuracy is", accuracy))

Dari hasil komputasi kami mendapatkan akurasi $0.913$ atau $91.3\%$, lebih baik dari target kami. Tentu saja seperti sebelumnya, ini hanya suatu projek sederhana mahasiswa dan tidak cukup baik digunakan di dunia nyata untuk digit recognition.

Kode lengkap bisa dilihat di sini. Thanks.

Referensi

• Lars Elden, 2007. Matrix Methods in Data Mining and Pattern Recognition.
• https://math.libretexts.org/Bookshelves/Linear_Algebra/Interactive_Linear_Algebra_(Margalit_and_Rabinoff)/06%3A_Orthogonality/6.03%3A_Orthogonal_Projection
• http://yann.lecun.com/exdb/mnist/
• https://en.wikipedia.org/wiki/MNIST_database