Dekomposisi Nilai Singular dan Kompresi Gambar

Sewaktu mengambil S2 di Bandung, semua mahasiswa diwajibkan untuk mengambil mata kuliah Analisis Matriks. Sebagai mahasiswa yang mengambil peminatan Aljabar saya tentu saja (terpaksa) menyukai mata kuliah tersebut. Dalam proses perkuliahan tersebut saya mengalami banyak kesulitan, saya ngerasa kalau mata kuliah itu banyak banget isi teorema dan bukti dan (menurut saya) contoh yang kurang. Padahal, saya adalah tipe yang menyukai buku Matematika dengan banyak contoh.

Salah satu bahasan di matkul Analisis Matriks adalah Dekomposisi Nilai Singular. Waktu di kelas, saya ngerasa bahwa bahasan ini cukup njelimet dengan banyak sifat yang harus dibuktikan sendiri. Tetapi setelah baca-baca ternyata dekomposisi matriks ini memiliki banyak aplikasi, salah satunya di bidang Statistik (Analisis Komponen Utama). Di tulisan ini saya ingin membahas mengenai Dekomposisi Nilai Singular dan sebuah toy example pengunaannya untuk kompresi gambar.

Open Table of Contents

Dekomposisi Nilai Singular
Kompresi Gambar
Referensi

Dekomposisi Nilai Singular

Secara Matematika, dekomposisi nilai singular adalah suatu cara untuk menuliskan sebarang matriks $A$ sebagai perkalian dari tiga buah matriks seperti yang diberikan di bawah ini.

Misal $A \in \mathbb{C}^{m \times n}, A \neq 0$ . Maka terdapat bilangan bulat positif $r$ , matriks diagonal $D \in \mathbb{C}^{r \times r}$ dengan unsur-unsur diagonal bilangan positif dan matriks dengan kolom-kolom ortonormal $U \in \mathbb{C}^{m \times r}, V \in \mathbb{C}^{n \times r}$ sedemikian sehingga $A = U D V^*.$

Suatu pernyataan yang sulit dipahami 😭. Jika kita misalkan $D = diag(\sigma_1, \ldots, \sigma_r)$ , $U = [u_1\ \ldots \ u_r]$ dan $V = [v_1\ \ldots\ v_r]$ , maka kita dapatkan pernyataan berikut ini yang disebut dengan ekspansi hasilkali luar dari $A$ yang lebih mudah untuk dibayangkan.

Misal $A \in \mathbb{C}^{m \times n}, A \neq 0$ . Maka terdapat himpunan ortonormal $\{ u_1,\ldots, u_r \}$ dan $\{ v_1,\ldots, v_r \}$ dan bilangan-bilangan positif $\sigma_1 > \sigma_2 > \cdots > \sigma_r$ sedemikian sehingga dapat kita tuliskan $A = \sum_{i=1}^r \sigma_i u_i v_i^*.$

Berdasarkan pernyataan di atas, kita dapat menyatakan sebarang matriks tak-nol $A$ sebagai penjumlahan dari matriks-matriks tak-nol yang masing-masing memiliki rank 1. Sebagai contoh, dengan mengambil dua buah vektor $u_i$ dan $v_i$ kita dapat merepresentasikan $A$ sebagai berikut.

$A \approx \sigma_1 \underbrace{\begin{bmatrix} \cdot\\ \vdots \\ \cdot \end{bmatrix}}_{u_1} \overbrace{[\cdot\ \cdots\ \cdot]}^{v_1^*} + \sigma_2 \underbrace{\begin{bmatrix} \cdot\\ \vdots \\ \cdot \end{bmatrix}}_{u_2} \overbrace{[\cdot\ \cdots\ \cdot]}^{v_2^*}$

Dengan kata lain, kita dapat menghampiri matriks $A$ dengan cara mengambil sebagian dari vekto-vektor $u_i$ dan $v_i$ (disebut dengan vektor singular) dan juga nilai $\sigma_i$ yang bersesuaian (disebut dengan nilai singular) dan melakukan proses penjumlahan seperti di atas. Semakin banyak vektor yang kita ambil maka hampiran yang kita peroleh akan semakin dekat dengan matriks awal yang kita miliki. Nilai $\sigma_i$ di atas menyatakan seberapa besar pengaruh dari vektor singular yang bersesuaian dalam menyatakan matriks awal.

Untuk kita bisa dapat bayangan apa yang dimaksud paragraf terakhir, kita masuk ke dalam contoh.

Kompresi Gambar

Kita akan menggunakan gambar kucing pada bagian atas tulisan ini sebagai contoh dari matriks yang akan kita dekomposisi. Kita ketahui bahwa suatu gambar merupakan perpaduan dari tiga buah layer yang masing-masing menyatakan warna merah, hijau dan biru. Untuk itu kita bagi gambar di atas menjadi tiga buah matriks yang menyatakan masing-masing warna.

import matplotlib.pyplot as plt
import numpy as np

# import picture
cat_image = plt.imread("cat_1920x1280.jpg")
plt.imsave("output_original.jpg", cat_image)

# Red Green and Blue layers
R = cat_image[:,:,0]
G = cat_image[:,:,1]
B = cat_image[:,:,2]

# print each layer
plt.subplot(1, 3, 1)
plt.imshow(R, cmap='Reds_r')
plt.subplot(1, 3, 2)
plt.imshow(B, cmap='Blues_r')
plt.subplot(1, 3, 3)
plt.imshow(G, cmap='Greens_r')

plt.savefig('cat_rgb.jpg')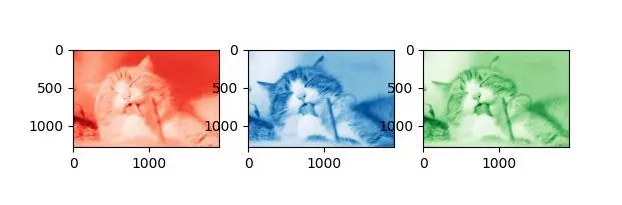

Yang akan kita lakukan adalah mendekomposisikan masing-masing matriks warna dengan SVD dan melihat pengaruh pengambilan vektor singular yang berbeda. Jika kita ambil 20 vektor singular pertama dan 40 vektor singular pertama kita akan dapatkan gambar berikut.

def show_image(i):
    R_compressed = np.array(np.matrix(U_R[:, :i]) * np.diag(S_R[:i]) * np.matrix(Vt_R[:i, :])).astype(np.uint8)
    G_compressed = np.array(np.matrix(U_G[:, :i]) * np.diag(S_G[:i]) * np.matrix(Vt_G[:i, :])).astype(np.uint8)
    B_compressed = np.array(np.matrix(U_B[:, :i]) * np.diag(S_B[:i]) * np.matrix(Vt_B[:i, :])).astype(np.uint8)

    im_new = np.stack((R_compressed, G_compressed, B_compressed), axis=2)
    plt.imshow(im_new)
    return im_new

cat_20components = show_image(20)
cat_20components = show_image(40)

Dapat kita lihat bahwa menggunakan 20 komponen pertama akan memberikan kita gambaran besar mengenai kucing pada gambar awal. Dengan menambahkan 20 komponen berikutnya kita memberikan detail-detail tambahan pada gambar kucing agar diperoleh gambar yang lebih serupa dengan gambar awal.

Jika kita hanya menggunakan komponen 21-40 tanpa menggambarkan 20 komponen pertama, kita dapatkan. image using components 20-40 Gambar di atas yang memberikan detail pada gambar sebelumnya. Dari gambar-gambar di atas, bisa kita lihat bahwa 20 komponen utama lebih dapat merepresentasikan gambar awal jika dibandingkan dengan 20 komponen berikutnya. Hal ini menunjukkan bahwa komponen-komponen awal memberikan informasi yang lebih banyak mengenai gambar (data) awal.

Lebih lengkapnya berikut adalah gambar yang diperoleh dengan menggunakan 10, 20, 40 dan 80 komponen pertama.

Gambar dengan 80 komponen sudah mendekati kualitas dari gambar awal dengan jumlah komponen yang lebih sedikit. Perbandingan ukuran file dari kedua gambar dapat kita peroleh sebagai berikut.

import os

print(str(os.path.getsize('cat_original.jpg')/1024) + " kilobytes")
print(str(os.path.getsize('cat_80components.jpg')/1024) + " kilobytes")

Dari perintah tersebut, ukuran file sebelumnya adalah 204kb sedangkan dengan gambar yang diperoleh dengan menggunakan 80 komponen adalah 164kb. Hal ini karena kita menggunakan lebih sedikit data untuk merepresentasikan gambar. Tetapi tentu saja pada kenyataannya untuk mengompresi gambar menjadi lebih kecil, kita akan menggunakan algoritma yang lebih kompleks dari ini.

Semua kode yang digunakan pada halaman ini dapat dilihat di sini. Thanks.

Referensi

Diktat Analisis Matriks. Pak Muchlis.
https://dmicz.github.io/machine-learning/svd-image-compression/